A while ago after I'd taken a few years of Calculus (nothing too advanced), I was frustrated at the vague and ambiguous definitions of "differentials" (dx, dy). I learned from the literature that it IS somewhat of an illusive concept.Ah, differentials. Differentials can be somewhat elusive, though, it bothers me that you received “vague and ambiguous definitions,” because the term “differential” is exactly what it sounds like: a difference, in this case, the difference between two points on a curve that define a line.
Liz, NY
We’re going to delve into some linear algebra here for a moment. Take the following function:
f(x)=x2
If you were to graph out this function, you would get a specific curve called a parabola:
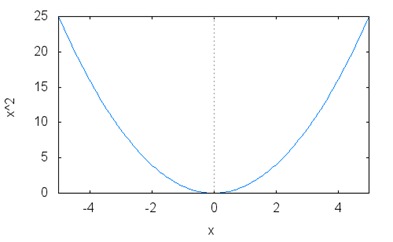
This parabola is the most basic curve in linear algebra, and it is usually the first introduced to students. Now, differentials are about tangents to this curve, and this all has to do with speed and acceleration. If the x axis represented time, and the y axis represented distance, then we could say that this curve could represent the distance traveled over time.
Let’s give a real world (okay, somewhat real world—all of the conditions presented here would have to be extreme circumstances, but I don’t make the rules) example to demonstrate what I mean.
Let’s pretend that we’re train engineers. A mysterious set of circumstances have occurred to damage our speedometer but not our odometer. We need to know what speed the train is travelling at any particular instant to know how much pressure to apply to the braking system. We do have a stopwatch, so the instant we start moving, we start the stopwatch. After 1 minute, we have gone 1 mile, so we write 1 min = 1 mile. After 2 minutes, we’ve gone 4 miles. After 3 minutes, we’ve gone 9 miles, and so on.
You’ll notice that if d = distance in miles and t = time in minutes, then the distance travelled would have to be d = t2. So how do we know the instantaneous speed at any time t? Well, we could say that the average speed overall is 9 miles / 3 minutes = 3 miles per minute. But that’s not the whole story. If at minute 2 we’ve gone 4 miles and at minute 3 we’ve gone 9 miles then the average speed between minutes 2 and 3 is:
5 miles per minute average speed between minutes 2 and 3. If you’ll notice, this formula is exactly the same as the formula for slope:
Well, that’s because it is. In linear algebra (and the calculus that springs from it), speed=slope.
So at the 3 minute mark, how fast are we really going? Let’s look at a table of varying times that will get arbitrarily closer and closer to t = 3 minutes.
| x2 | x1 | f(x2) | f(x1) | average speed |
| 3 | 2.5 | 9 | 6.25 | 5.5 |
| 3 | 2.75 | 9 | 7.5625 | 5.75 |
| 3 | 2.85 | 9 | 8.1225 | 5.85 |
| 3 | 2.95 | 9 | 8.7025 | 5.95 |
| 3 | 2.975 | 9 | 8.850625 | 5.975 |
| 3 | 2.99 | 9 | 8.9401 | 5.99 |
| 3 | 2.999 | 9 | 8.994001 | 5.999 |
| 3 | 2.9999 | 9 | 8.9994 | 5.9999 |
| 3 | 2.999999 | 9 | 8.999994 | 5.999999 |
If you’ll notice, the closer x1 gets to x2, the closer the average speed gets to 6 but not quite. Why? Because there’s a problem in the formula used to determine this speed:
If x2 ever equals x1, then the denominator in this formula becomes 0, a condition that is undefined and causes the universe to collapse into a massive black hole.
So let’s define a new variable: Δx (read “delta x”) and define Δx as being x2-x1. And we also need something to stop Δx from becoming 0, thus saving the universe. This is called a “limit,” and we symbolize it like this:
And what we’re doing is getting the slope of the tangent of f(x) at an arbitrary point, so we’d symbolize that as:
So our new formula would look like this:
Since we’ve defined f(x) as being equal to x2, let’s see how this plays out.
So, now we know exactly how fast our train is going at 3 minutes, and can verify that it is, indeed going 6 miles per minute, since x=3, and 2x=6.
To bring it back to the original question: a differential is defined specifically as follows:
A differential is the difference between two points on a curve, producing a slope. As the differential approaches zero, the resultant slope gets closer to representing the slope of the tangent to the curve at a particular point.In other words: Δx.
I know I’ll be laughed out of my Math Club, but I cannot recommend Calculus for Dummies by Mark Ryan enough. It’s superbly written, and fully explains in plain English these concepts and many more.
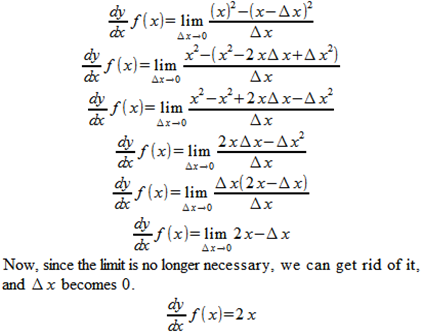
This is an excellent explanation of the rudiments of calculus and how quantities approach zero. A tangent is a line not a point, so there's gotta be distance on both coordinates to make the line. But as the line shrinks, it gets closer to the point, which is on the function. So dx and dy are the height and width of the triangle shrinking down to the point; the y displacement for the linear function (slope) over the x displacement from the fixed point. All good here. The terminology causes confusion, because sometimes they are treated as actual quantities and can be multiplied and such, or divided and seen as a fraction. But in some cases it's like the notation is just a written convention (as first year calc teachers can tell you)...and basic questions for the student can arise like "Is dx/dy a written convention for derivative, and does "dx/dy f(x)" mean "the derivative of f(x)" [as opposed to writing f'(x) or something]? Or does it mean some fraction times f(x)? It's both, I believe. But then you get notation like ∫ d/dx f(x) dx = f(x), and you're like "what the fuck does that "d" mean now? KILL ME!!". At this point I think I get it. And I believe that some of the notational conventions can cause confusion for students.
ReplyDeleteAnd then there's the whole chain rule where differentials start to do funny things because composite functions rescale them. But I'll have another long rant for that. ;)
Just so you know, the correct notation is "dy/dx" (I initially made the same mistake which I've now corrected). It is just a notation, but an important one, because it represents what you are doing when you find a derivative: dividing the difference (d) along the y-axis by the difference (d) along the x-axis. f'(x) (read "f-prime of x") is shorthand for dy/dx f(x).
ReplyDelete