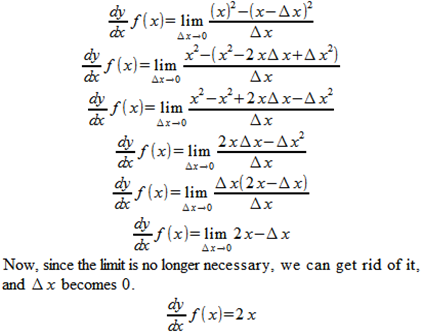A Pythagorean triple is a solution to the Pythagorean Theory such that . For example, {3, 4, 5} is a Pythagorean triple because . This becomes important when discussing complex numbers of the form . The reason is that the Pythagorean theorem applies to complex numbers, too, because and above are the legs of a right triangle. The length of the hypotenuse of such a triangle is equal to . This is also called the "magnitude" or "absolute value" of the complex number, and it represents the distance of the complex number from 0. It is frequently abbreviated . Now, if you take a Pythagorean triple such as , and multiply it by another pythagorean triple, say and multiply them together: Here's what's amazing: 33 and 56 are themselves legs of a Pythagorean triple! The reason this works blew my mind (#CLICKBAIT). Multiplying two complex numbers also multiplies their magnitudes, so: This is true of all complex numbers. Now, let's say that and then since is algebraically closed for multiplication, it makes sense that . Also, since then it follows that . So, in the new triangle, we have both legs of integer length and a hypotenuse of integer length. This is the very definition of a Pythagorean triple.

All Was Quiet on New Year's Day

A nameless friend writes:

Tom, What is the most common day of the week for New Year's Day to fall on?

The answer might surprise you.

First, let me explain for the uninitiated out there how the Gregorian Calendar works.
From the Wikipedia article:

The Gregorian calendar, also known as the Western calendar, or Christian calendar, is the internationally accepted civil calendar.^[1][2][3] It was introduced by Pope Gregory XIII, after whom the calendar was named, by a decree signed on 24 February 1582, a papal bull known by its opening wordsInter gravissimas.^[4] The reformed calendar was adopted later that year by a handful of countries, with other countries adopting it over the following centuries. The motivation for the Gregorian reform was that the Julian calendar assumes that the time between vernal equinoxes is 365.25 days, when in fact it is presently almost exactly 11 minutes shorter. The error between these values accumulated at the rate of about three days every four centuries, resulting in the equinox occurring on March 11 (an accumulated error of about 10 days) and moving steadily earlier in the Julian calendar at the time of the Gregorian reform. Since the Spring equinox was tied to the celebration of Easter, the Roman Catholic Church considered that this steady movement in the date of the equinox was undesirable.
[snip]

The Gregorian calendar modified the Julian calendar's regular cycle ofleap years, years exactly divisible by four,^[6]including all centurial years, as follows:

Every year that is exactly divisible by four is a leap year, except for years that are exactly divisible by 100; the centurial years that are exactly divisible by 400 are still leap years. For example, the year 1900 is not a leap year; the year 2000 is a leap year.^[7]

In addition to the change in the mean length of the calendar year from 365.25 days (365 days 6 hours) to 365.2425 days (365 days 5 hours 49 minutes 12 seconds), a reduction of 10 minutes 48 seconds per year, the Gregorian calendar reform also dealt with the past accumulated difference between these lengths. Between AD 325 (when the Roman Catholic Church thought the First Council of Nicaea had fixed the vernal equinox on 21 March), and the time of Pope Gregory's bull in 1582, the vernal equinox had moved backward in the calendar, until it was occurring on about 11 March, 10 days earlier. The Gregorian calendar therefore began by skipping 10 calendar days, to restore March 21 as the date of the vernal equinox.

Cite: Gregorian calendar. (2012, January 11). In Wikipedia, The Free Encyclopedia. Retrieved 23:45, January 12, 2012, from http://en.wikipedia.org/w/index.php?title=Gregorian_calendar&oldid=470859503

Here's an interesting trick: What day of the week will Jan 1, 2400 fall on?  Answer: Saturday.  Every four hundred years the calendar resets itself and begins on a Saturday.  The reason is simple:


365.2425 × 400 = 20871, which is evenly divisible by 7. 


That means that New Year's Day of any year divisible by 400 will always be Saturday.  January 1, 2000, was on a Saturday, and January 1, 4000, will be on a Saturday.


That also means that years 400 years apart will begin on the same day: January 1, 2012, for example, was on a Sunday, and so will January 1, 2412.


This all means that in order to find out what the most common day of the week New Year's Day falls on, we need to analyze 400 years worth of New Year's Days.

Here is the table:

Days of week	Count
Sun	58
Mon	56
Tue	58
Wed	57
Thu	57
Fri	58
Sat	56
Grand Total	400

So the answer to your question is a three-way tie: Sunday, Tuesday, and Friday are the most common days for New Year's Day to fall on, but not by much.

Hexagons, part I

We interrupt our regularly scheduled series to present to you the amazing hexagon.

Here is a regular hexagon:

You might say, “Tom, what’s so special about a hexagon?” Let me tell you:

1. It has the most number of sides (6) of any regular polygon that can be tiled (there other polygons with more sides such as some decagons that can be tiled, but they won’t be “regular”).
2. They have a very special relationship to circles, which I will get into at a later time.
3. Hexagons appear in nature in many places and ways:
1. A honeycomb is made of hundreds or thousands of hexagons;
2. The north pole of Saturn has a hexagonal cloud pattern.
3. Snowflakes have hexagonal crystal structures.

The fact of the matter is, hexagons appear in nature so much because they make efficient use of space.

Here’s an interesting fact about regular hexagons.  Let’s take a regular hexagon and draw a circle around it such that the vertices of the hexagon are all on the circle’s edge, like so:

Let me tell you an interesting property of the hexagon in the above figure: the sides of the hexagon are all equal to the radius of the circle it inscribes!

So, we’re going to talk about hexagons a little.

Differentials–The Elusive Concept?

A friend to Tom’s Math Class writes:

A while ago after I'd taken a few years of Calculus (nothing too advanced), I was frustrated at the vague and ambiguous definitions of "differentials" (dx, dy). I learned from the literature that it IS somewhat of an illusive concept.
Liz, NY

Ah, differentials.  Differentials can be somewhat elusive, though, it bothers me that you received “vague and ambiguous definitions,” because the term “differential” is exactly what it sounds like: a difference, in this case, the difference between two points on a curve that define a line.

We’re going to delve into some linear algebra here for a moment.  Take the following function:

f(x)=x²


If you were to graph out this function, you would get a specific curve called a parabola:



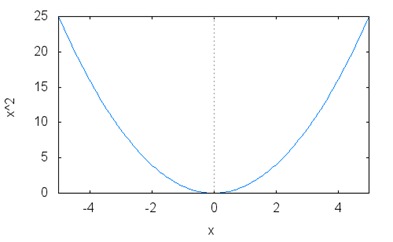
This parabola is the most basic curve in linear algebra, and it is usually the first introduced to students.  Now, differentials are about tangents to this curve, and this all has to do with speed and acceleration.  If the x axis represented time, and the y axis represented distance, then we could say that this curve could represent the distance traveled over time.

Let’s give a real world (okay, somewhat real world—all of the conditions presented here would have to be extreme circumstances, but I don’t make the rules) example to demonstrate what I mean.

Let’s pretend that we’re train engineers.  A mysterious set of circumstances have occurred to damage our speedometer but not our odometer.  We need to know what speed the train is travelling at any particular instant to know how much pressure to apply to the braking system.  We do have a stopwatch, so the instant we start moving, we start the stopwatch.  After 1 minute, we have gone 1 mile, so we write 1 min = 1 mile.  After 2 minutes, we’ve gone 4 miles.  After 3 minutes, we’ve gone 9 miles, and so on. 

You’ll notice that if d = distance in miles and t = time in minutes, then the distance travelled would have to be d = t².  So how do we know the instantaneous speed at any time t?  Well, we could say that the average speed overall is 9 miles / 3 minutes = 3 miles per minute.  But that’s not the whole story.  If at minute 2 we’ve gone 4 miles and at minute 3 we’ve gone 9 miles then the average speed between minutes 2 and 3 is:



5 miles per minute average speed between minutes 2 and 3.  If you’ll notice, this formula is exactly the same as the formula for slope:



Well, that’s because it is.  In linear algebra (and the calculus that springs from it), speed=slope.
So at the 3 minute mark, how fast are we really going?  Let’s look at a table of varying times that will get arbitrarily closer and closer to t = 3 minutes.

x2	x1	f(x2)	f(x1)	average speed
3	2.5	9	6.25	5.5
3	2.75	9	7.5625	5.75
3	2.85	9	8.1225	5.85
3	2.95	9	8.7025	5.95
3	2.975	9	8.850625	5.975
3	2.99	9	8.9401	5.99
3	2.999	9	8.994001	5.999
3	2.9999	9	8.9994	5.9999
3	2.999999	9	8.999994	5.999999

If you’ll notice, the closer x₁ gets to x₂, the closer the average speed gets to 6 but not quite.  Why?  Because there’s a problem in the formula used to determine this speed:

If x₂ ever equals x₁, then the denominator in this formula becomes 0, a condition that is undefined and causes the universe to collapse into a massive black hole.

So let’s define a new variable: Δx (read “delta x”) and define Δx as being x₂-x₁.  And we also need something to stop Δx from becoming 0, thus saving the universe.  This is called a “limit,” and we symbolize it like this:



And what we’re doing is getting the slope of the tangent of f(x) at an arbitrary point, so we’d symbolize that as:



So our new formula would look like this:

Since we’ve defined f(x) as being equal to x², let’s see how this plays out.



So, now we know exactly how fast our train is going at 3 minutes, and can verify that it is, indeed going 6 miles per minute, since x=3, and 2x=6.

To bring it back to the original question: a differential is defined specifically as follows:

A differential is the difference between two points on a curve, producing a slope.  As the differential approaches zero, the resultant slope gets closer to representing the slope of the tangent to the curve at a particular point.

In other words: Δx.

I know I’ll be laughed out of my Math Club, but I cannot recommend Calculus for Dummies by Mark Ryan enough.  It’s superbly written, and fully explains in plain English these concepts and many more.

Symbolic Logic 3: The Or Operator

In the last post, we discussed the “And” operator (symbolized as “∧” as in “P ∧ Q”).  Today, we’re going to discuss its brother, “Or.”
Similar to the And operator, Or is symbolized thusly:

P∨Q

And just like And, an Or statement can be evaluated to True or False.  The difference with Or is that it evaluates to False only if both component statements are False.  Here is the truth table for P∨Q

P	Q	P ∨ Q
True	True	True
True	False	True
False	True	True
False	False	False

The definition of the “Or” operator could be this:

The “Or” operator evaluates to False if and only if both component operands are False.

If you’ll recall, we had values for P and Q:

P=”The car is green”
Q=”The car has four doors.”

So P ∨ Q would read as:

Either the car is green or it has four doors, or both.

If our hypothetical car has two doors, this statement is still true, because both predicates must evaluate to False in order for the whole thing to be False.  In fact, let’s look at the truth table for this statement, just for fun:

Either the car is green or it doesn’t have four doors, or both.

That would be symbolized like this:

P ∨ ~Q

Here’s the truth table of that statement:

P	Q	~Q	P∨~Q
True	True	False	True
True	False	True	True
False	True	False	False
False	False	True	True

This is interesting.  This statement seems to be false only if it has four doors, but it isn’t green.  Might there be a causal relationship here?  Let’s look at this another way.  Let’s say P=”The car is a coupe.” and Q=”The car is fast.”  P ∨ ~Q seems to imply that in order for you to have a fast car, it must be a coupe.  That seems to say something wholly different.  I’ll cover that in my next post.
Next: Differentials
Next in the Logic Series: The If… Then Operator

Symbolic Logic, Part II: The “And” Operator

In the last post, we discussed the statement P, which we defined as “The car is green,” and how the statement is either True, or it is False.  We also talked about “not P”, which we symbolized as ~P.

Now, let’s say we have another statement:

The car has four doors.

We’re going to call this statement Q. It also has two possible states: True and False. Here is its truth table:

Q

True

False

And here is the truth table for Q and ~Q:

Q	~Q
True	False
False	True

Now we can combine P and Q to create a compound statement thusly:

The car is green and it has four doors.

We are going to symbolize this conjunction like so:

P ∧ Q

That little upside-down “V” between P and Q represents the operator “and,” and the statement as a whole would be read “P and Q.” Now, P∧Q also evaluates as a whole statement to either True or False, but this depends on the values of both P and Q. In the case of the ∧ operator, both P and Q must be True for P∧Q to be True. Here is the truth table for this:

P	Q	P∧Q
True	True	True
True	False	False
False	True	False
False	False	False

So, if we say P∧Q, but the car actually has two doors, then it doesn’t really matter what color the car is, the entire statement is false.  The rule of the “And” operator is this:

A compound statement using the “And” operator evaluates to True if and only if both component statements are True; otherwise, the compound statement is False.

If we were going to say that:

The car is green and does not have four doors.

We would symbolize it thusly:

P ∧ ~Q

And the truth table would look like this:

 

P	Q	~Q	P ∧ ~Q
True	True	False	False
True	False	True	True
False	True	False	False
False	False	True	False

So, in the case of our hypothetical two-door, green car, P ∧ ~Q will evaluate to True, since it is true that the car is green and it does not have four doors.  Note that this statement is also True if the car has five doors, or three doors, or anything other than four doors.

Next: The “Or” Operator

Symbolic Logic, part I: Introduction to Basic Concepts

One important area of math is “symbolic logic,” which is also known as “formal logic” or sometimes “Boolean algebra.”
Here’s how it starts.  I’m going to start with a statement:

The car is green.

We are going to call this statement P.  Note that when we say “statement,” we mean something that is factual, not opinion.  So “The car is green” is okay (as long as we agree what “green” is: but, I digress), but “The car is beautiful” is not.  Our statement P can have one of two states: It can either be True or it can be False.  If we were to put these possible values into a table, they would look like this:

P

True

False

It may seem a bit silly to have such a table, but I’m introducing it here to introduce the concept of the “Truth table.” This is the truth table of the statement P.

Note that there is no “Maybe” listed here.  That’s because in logic, a statement is either totally true or it is totally false.  There is no middle ground; the car is either green or it is not.  If it’s “kinda” green, then it’s not green, and the statement would be false.  Now, we could get into arguments about the definition of “green,” and get into specific color wavelengths on the electromagnetic spectrum, but for our purposes, green is green, and a car is either green or it isn’t.

Then there is this statement:

The car is not green.

We could call this statement “not P.”  We would symbolize it thusly: ~P.  Whenever P is True, ~P is false, and vice versa.  The truth table would look like this:

P	~P
True	False
False	True

Next: We will be introducing compound statements.